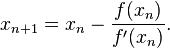shaunhess.com - Journal

In the last post we looked at the Bisection Method to solve a simple problem, finding the square root of a real number. This week we are going to use the same exact problem, but use a better algorthim.

Newton's method (also known as the Newton–Raphson method), named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots (or zeroes) of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method.

The Newton-Raphson method in one variable:

Given a function ƒ(x) and its derivative ƒ '(x), we begin with a first guess x₀ for a root of the function. Provided the function is reasonably well-behaved a better approximation x₁ is

$x_{1} = x_0 - \frac{f(x_0)}{f'(x_0)}.\,\!$

Geometrically, x₁ is the intersection with the x-axis of a line tangent to f at f(x₀).

The process is repeated until a sufficiently accurate value is reached:

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}.\,\!$

So basically we start with an initial guess, find the tangent where it crosses the x axis as the next guess, and iterate.

So lets define a function to find a square root using this method:

function squareRootNR {            
 Param(            
  [parameter(Position=0,             
  Mandatory=$true,             
  HelpMessage="Enter a non-negative number." )]             
  [ValidateScript({$_ -gt 0})]             
  [float]$x,            
  [parameter(Position=1,             
  Mandatory=$true,             
  HelpMessage="Enter upper bound on the relative error." )]             
  [ValidateScript({$_ -gt 0})]            
  $epsilon            
 )            
             
 $guess = $x / 2.0            
 $diff = [Math]::Pow($guess,2) - $x            
 $ctr = 1            
             
 while ([Math]::Abs($diff) -gt $epsilon -and $ctr -lt 100) {            
  $guess = $guess - $diff / (2.0 * $guess)            
  $diff = [Math]::Pow($guess,2) - $x            
  $ctr += 1            
 }            
             
 if ($ctr -ge 100) {            
  Write-Warning "Iteration count exceeded."            
 }            
             
 Write-Host "NRMethod. Number of Iterations was:", $ctr, " and Estimate is: ", $guess            
 return $guess            
}

PS H:\Development\Powershell> squareRootNr -x 9 -epsilon 0.000001 NRMethod. Number of Iterations was: 5 and Estimate is: 3.00000000003932 3.00000000003932

Lets compare this against our last attempt using the Bisection method:

PS H:\Development\Powershell> squareRootBi -x 9 -epsilon 0.000001 BiMethod. Number of Iterations was: 25 and Estimate is: 3.00000008940697 3.00000008940697

As you can see we need much fewer iterations to solve the same problem.